
Basics of flow measurement
The flow of a gas or liquid is measured for a variety of reasons, certainly including commercial considerations as part of a contract and also in various production processes. The flow or volume flow (volume/time) can be recorded, among other things, by the measured value of pressure.
Volume flow can be measured using various methods. In addition to ultrasonic flow sensors, these include magnetic-inductive flow sensors and sensors that work according to the differential pressure method, among these being the orifice plate, Venturi nozzle and the Prandtl pitot tube. When evaluating the measured values, the Bernoulli equation is used for all sensors operating on the differential pressure method:
Q = V/t = VmA
Q = volume flow
Vm = median velocity
t = time
A = area
V = volume
We will now take the measurement of volume flow using an orifice plate as the example. By attaching the plate to a pipe, this then becomes narrowed at one point.
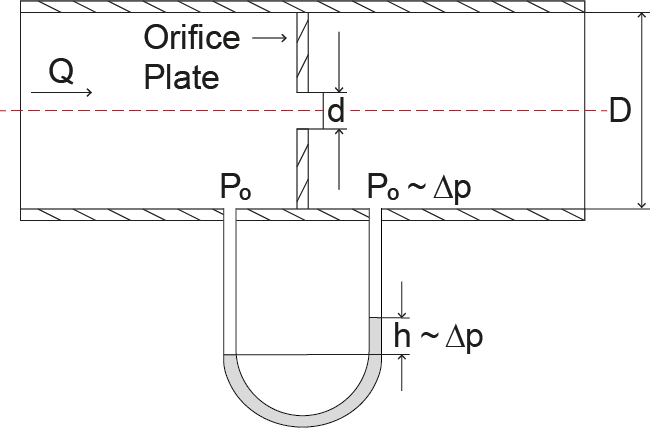
Image 1: Orifice plate
With a smooth flow, the same pressure should prevail both before and after the orifice plate:
p1 + ½ ρv12=p2+ ½ ρv22
p = pressure
ρ = density
v = velocity
This assumption is based on the continuity equation, which states that everything flowing into a pipe eventually also comes out:
v1A1 = v2A2
v = velocity
A = area

Image 2: Flow measurment
Under realistic conditions, however, friction occurs, which then leads to a pressure drop:
p + ½ ρv2 + wR = constant
p = pressure
ρ = density
v = velocity
wR = rate of frictional force by volume

Image 3: Pressure drop
This pressure drop is important in determining the volume flow. The friction effect itself, however, depends upon many factors. For this reason, an empirical formula is used, which in turn relies on empirical values. The volume flow now ultimately results from the root of the pressure differential:
Q = 4000 αεd2√∆p/ρ
Q = volume flow
α = empirical flow coefficient
ε = expansion factor
d = internal orifice diameter
∆p = pressure differential
ρ = density
To make this formula a little easier for users, all of the constant values from the measuring system and the measuring medium can be summed up as the constant ‘c’. The result for a fluid, for example, then offers the equation:
Q = c √∆p

