Characteristic curve, hysteresis, measurement error: Terminology in pressure measurement technology

Characteristic curve, hysteresis, measurement error: Terminology in pressure measurement technology

by | Tuesday, 30 June, 2020 | Pressure Measurement

The first data sources for users of pressure measurement technology are often the data sheets supplied by the manufacturers. Of particular interest here is usually the accuracy data. In this context, a large number of terms appear whose comprehension is of great importance in assessment of that particular measurement instrument.

On the topic of accuracy, it can be fundamentally stated that the term itself is not subject to any defined standard. This, however, is not the case for the terminology arising in association with accuracy specifications, including characteristic curve, hysteresis, non-linearity, non-repeatability, and measurement error. In the following, we will briefly explain these terms.

Characteristic curve

The characteristic curve indicates the dependence of the output signal (measured value) upon the input signal (pressure). In the ideal scenario, the characteristic curve will be a straight line.

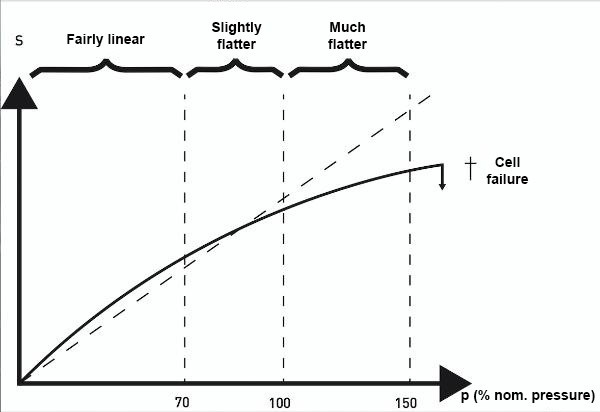
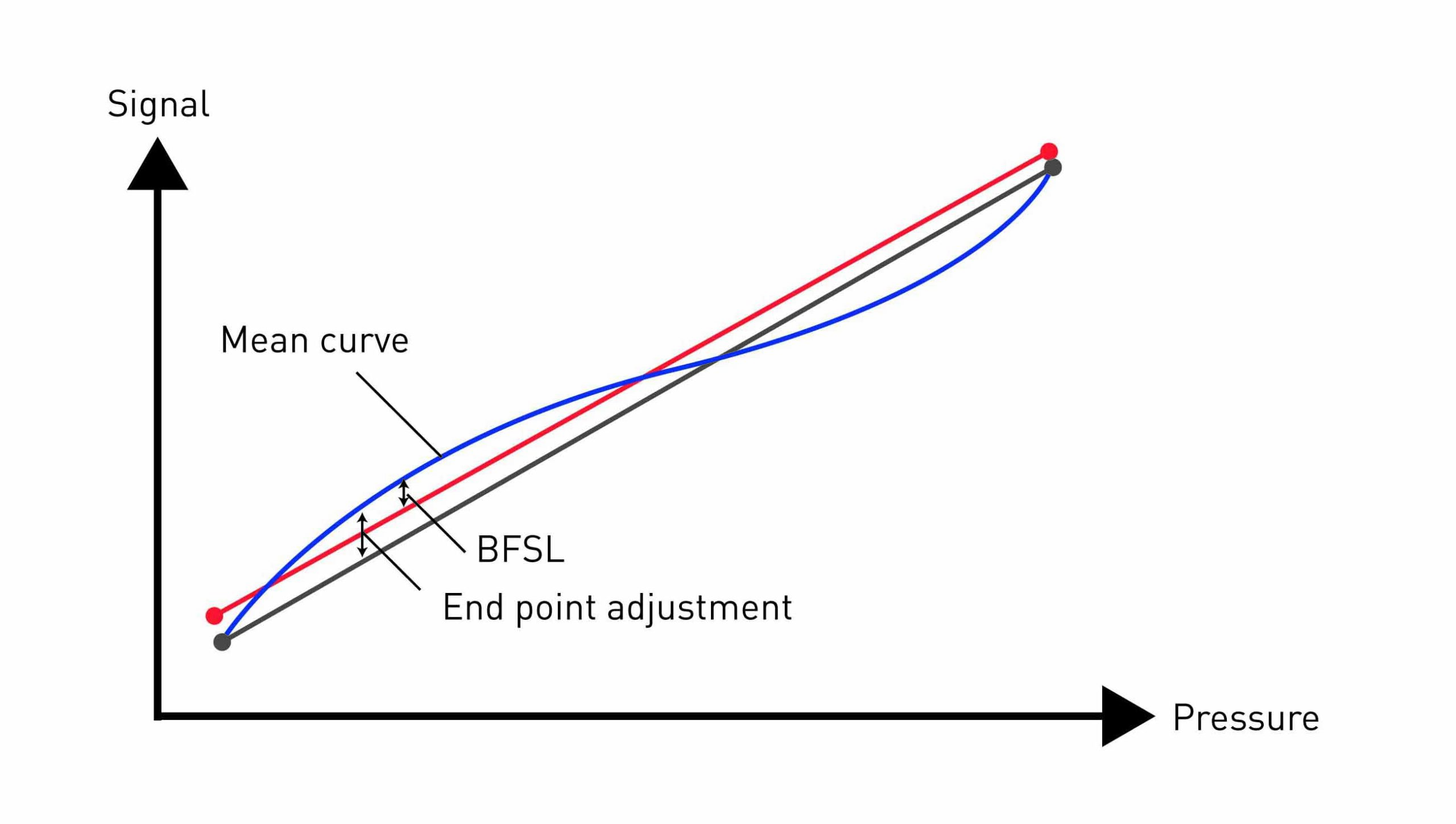
Non-linearity

The greatest deviation (positive or negative) of the characteristic curve from a reference line is described as non-linearity. The reference line itself can be determined by three different methods: End Point adjustment, Best Fit Straight Line(BFSL) and Best Fit Through Zero. Each of these methods arrives at different results, with Limit Point adjustment being the most commonly used method in Europe. The reference line here runs through the start and end point of the characteristic curve.

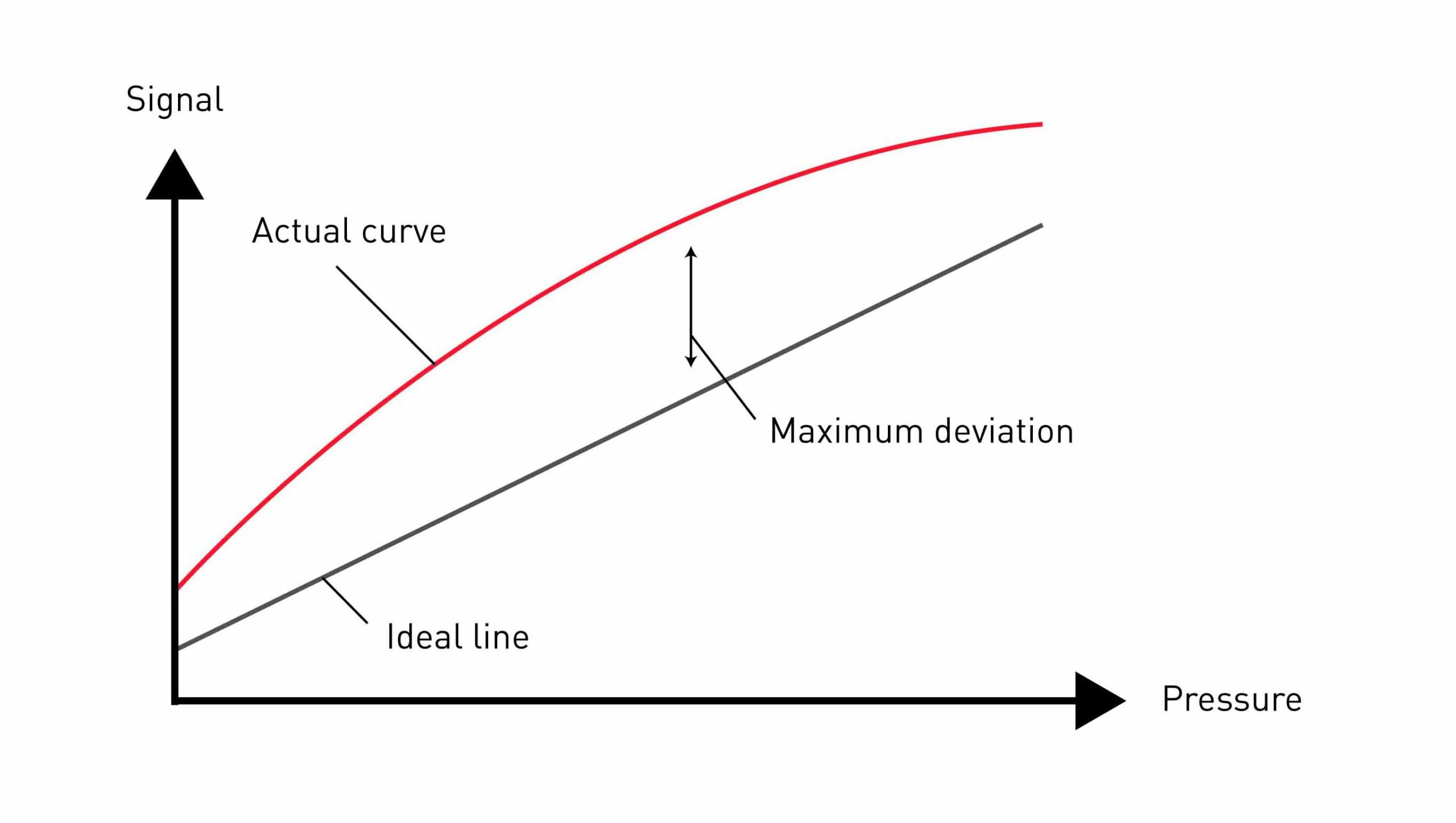
Measurement error

The measurement error, or measurement deviation, describes the shift of the displayed value from the “correct” value. This “correct” value is an ideal one, which in practice can only be attained with a highly accurate measuring device under reference conditions, such as a primary standard as would be used in calibration. The measurement error is expressed as either an absolute or a relative error. Absolute error is listed in the same units as the measured value, whereas relative error refers to the correct value and remains unit-free.

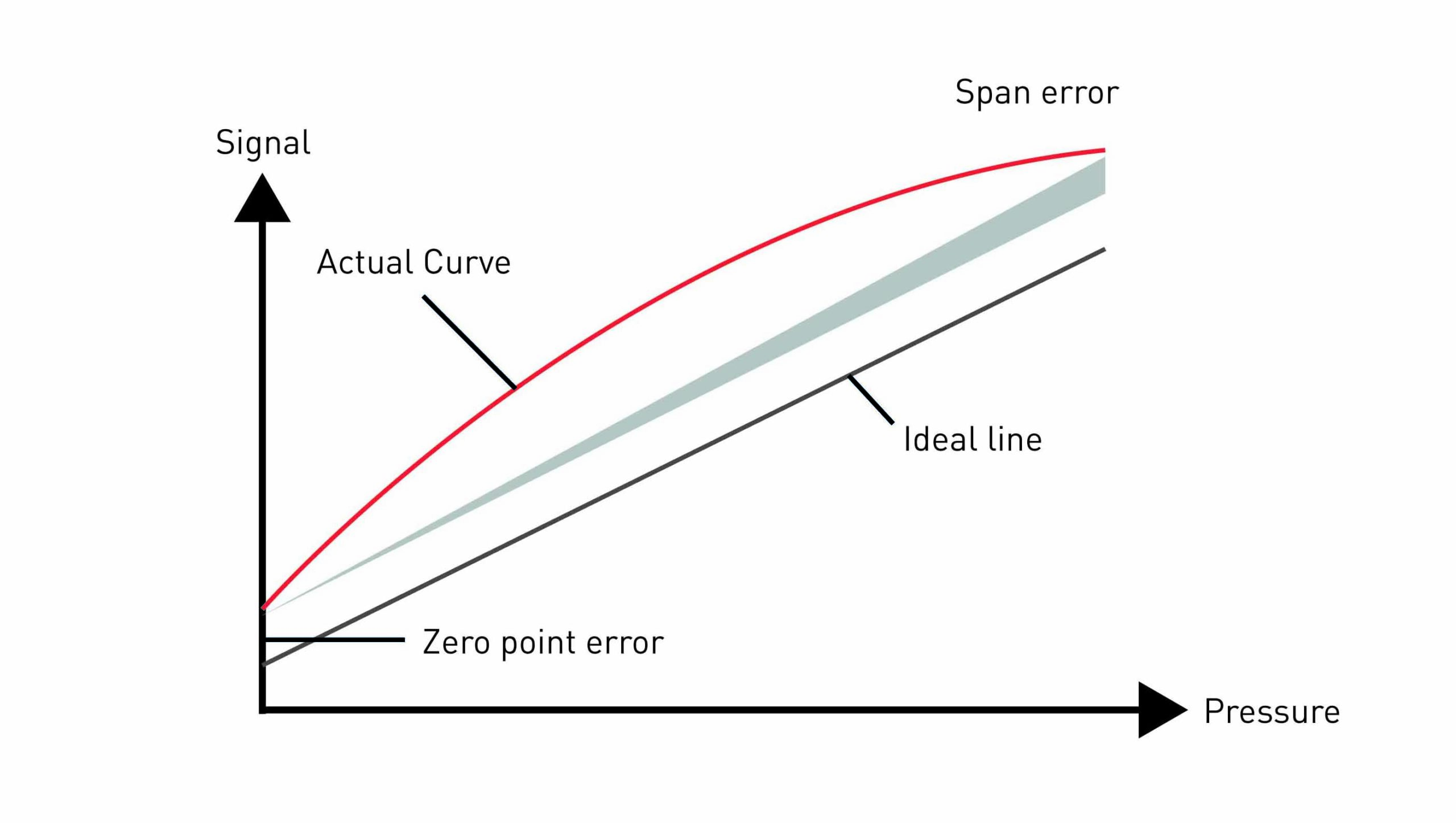
Zero point and span errors

In sensor production, there are deviations from the reference device (standard). Measurement deviations at the measuring range start and end points are referred to as zero point and span errors. The latter relates to the difference between the two values. The zero point error is the difference between the ideal zero point of the target characteristic line and the true output value of the actual characteristic curve.

Zero point error can be easily read off by the user in an unpressurized state. In order to eliminate it, the user must then enter this as an offset into the evaluation unit. Elimination of the span error is somewhat more difficult, since the pressure at the end of the measuring range must be approached precisely.

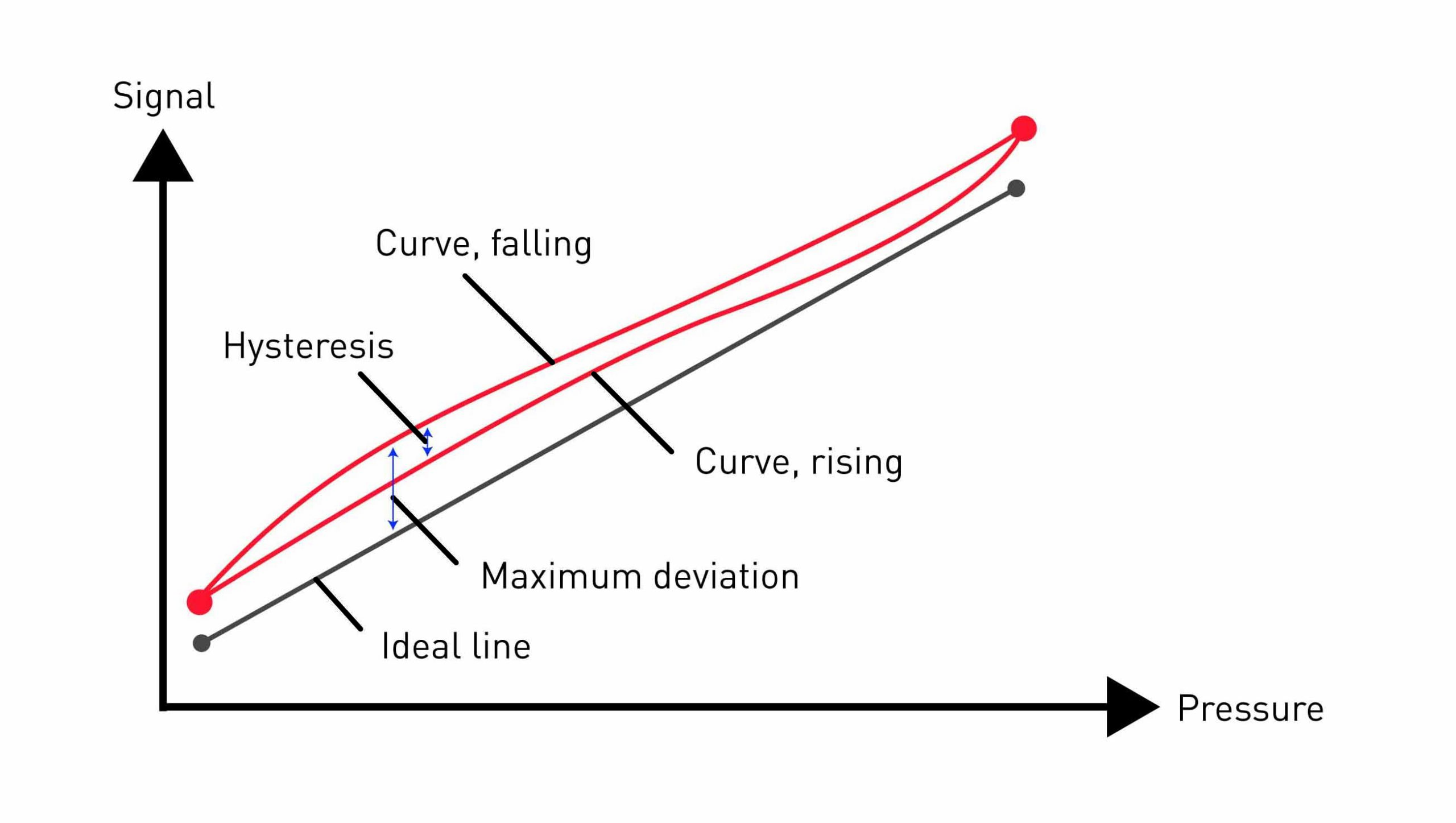
Hysteresis

The displayed value measured depends not only on the input variable (here, pressure), but also on the values measured previously from the input variable.

If the characteristic curve of the measuring device is recorded with continuously increasing pressure and then compared with the characteristic curve at continuously decreasing pressure, it is noticeable that the output signals, despite identical pressures, are not themselves exactly identical. The maximum deviation between these two characteristic curves is termed hysteresis and is expressed as a percentage of full scale (% FS).

Non-repeatability

Even when measured under identical conditions, electronic pressure transmitters are subject to stochastic influences, because of which the output signal is not identical at the same pressure values over successive measurements. The biggest deviation over three successive measurements taken from the same direction of approach is thus expressed as non-repeatability. A reliable pressure measuring device is recognized by users from its lowest possible non-repeatability.

Similar to hysteresis, non-repeatability cannot be compensated for.

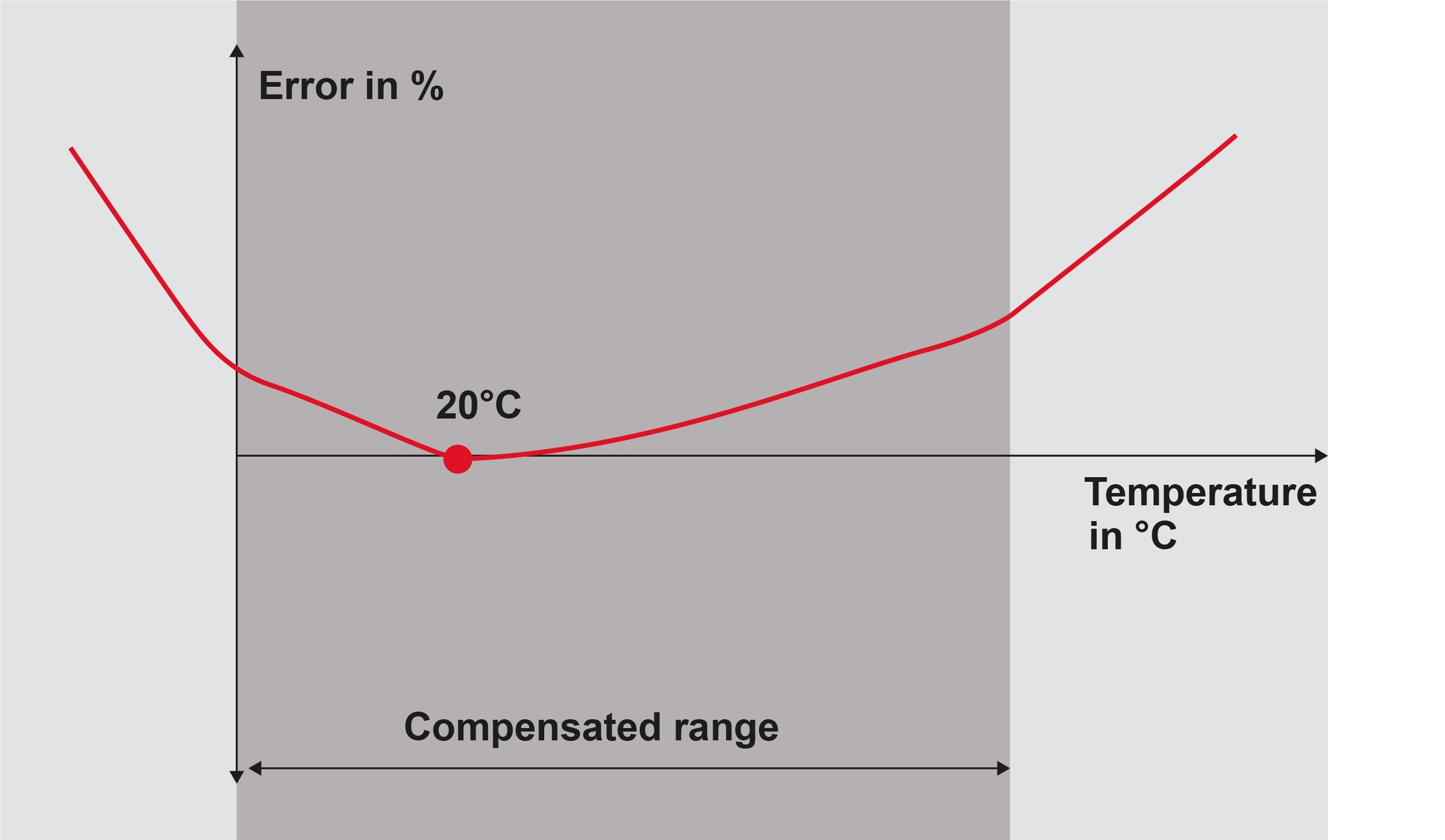
Temperature error

Temperature changes directly affect the characteristics of a pressure sensor. The electrical resistance of semiconductors, as used in piezoresistive pressure transmitters, decreases with increasing temperature, for example. Manufacturers therefore optimize their products by way of a balanced thermal characteristic. Temperature-related errors are either compensated for directly on the sensor or are performed electronically. Some devices also have a temperature sensor that directly compensates for these temperature-related errors. All the same, errors such as this can only be minimized but not completely eliminated. This residual temperature error is indicated by some manufacturers as a temperature coefficient.

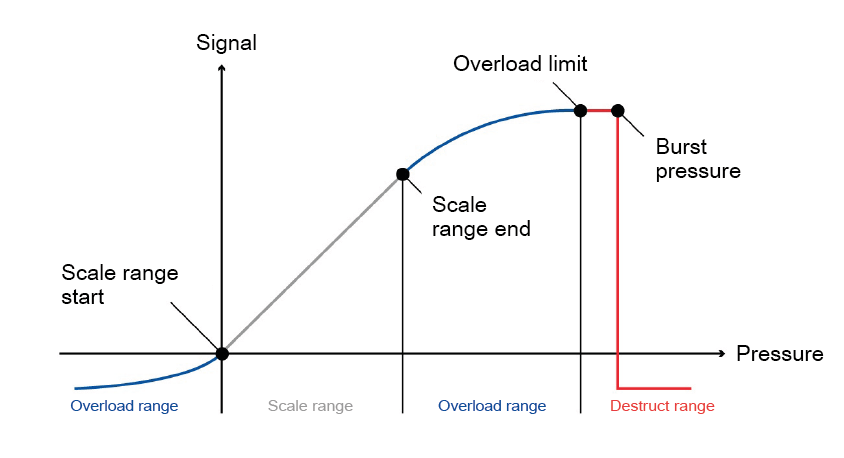
Overload pressure – Overpressure

The specified error limits are exceeded into the overload range. The pressure transmitter, however, suffers no lasting damage.

Burst pressure

The burst pressure indicates the pressure at which deformation of the pressure transducer occurs, where it becomes mechanically damaged.

Long-term stability

External influences affect the measuring instrument. For this reason, the characteristic curve does not remain constant over years of use. The long-term stability (also long-term drift) is determined by manufacturers under laboratory conditions and listed in data sheets as a percentage of full scale per annum.

The actual operating conditions of the device can however differ significantly from the test conditions. Test procedures between manufacturers can also vary widely, which makes comparability of the data even more difficult. In general, it is recommended that the pressure transducer be calibrated at regular intervals and, if necessary, adjusted.

Accuracy: Non-conformity of a curve

As mentioned at the outset, “accuracy“ is not a fixed value. Another term occasionally used for accuracy is non-conformity of a curve. This describes the maximum total error according to IEC 770 and comprises the linearity deviation and hysteresis, as well as non-repeatability. It is therefore the deviation from the ideal characteristic line at the end value of the measurement range and is expressed as a percentage.

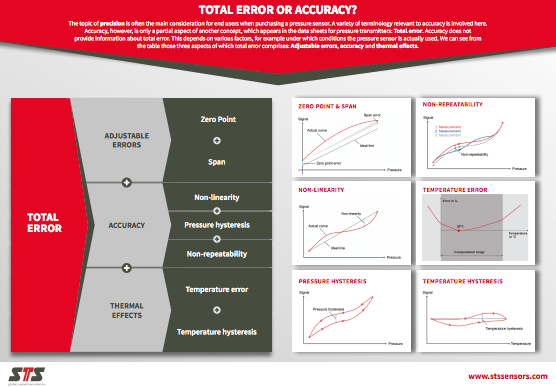
Download the free STS infographic on total error here:
Contact
The pressure response of piezoresistive pressure sensors

The pressure response of piezoresistive pressure sensors

by | Tuesday, 30 June, 2020 | Pressure Sensor Technology

Piezoresistive pressure sensors stand out for their high sensitivity. Also in terms of precision and miniaturization, many advantages arise over other measurement instruments. In our knowledge article, we will be explaining the pressure response of piezoresistive pressure sensors.

Users of piezoresistive pressure transducers expect a linear pressure response, in which the output signal is proportional to the applied pressure. For this reason, the curve of the pressure-signal diagram should be a straight line, whose starting point is indicated by the zero position and its sensitivity by the gradient. The true shape of the pressure-signal curve, however, more or less always shows a sharp deviation from the ideal line. This discrepancy is known as the linearity error of the pressure sensor. The gradient of the curve, on the other hand, corresponds to its sensitivity.

We can see from the illustration that a virtually linear part of the curve is utilized when the sensor is used at lower sensitivities (ca. 70% of the nominal chip pressure). Through selection, transmitters can be built of a very low non-linearity (think 0.05 %FS). The prerequisite, however, is that the operating range lies within the linear part of the chip.

The sensitivity of piezoresistive pressure sensors

The sensitivity of a pressure transducer largely depends upon two factors:

  • the resistive value of the diffused semiconductor resistors and their piezoresistive effectiveness level,
  • the thickness of the silicon diaphragm.

The greatest influence upon pressure response lies in the thickness of the silicon diaphragm. This is defined by its mechanical, chemical or even combined processing. These processes cannot be so precisely controlled that all pressure measurement cells exhibit the exact same sensitivity. Classes are thus established within which the pressure sensors can be used for a particular pressure range. And within these classes, sensitivities can vary by around ±20%. This deviation itself can be compensated for in the electronics through the supply current or the amplification factor (calibration).

The linearity of piezoresistive pressure sensors

It should be noted in linearity specifications that %FS (full scale, final value) is mostly applied. In terms of measured value, the error can carry quite significant weight, even when the manufacturer specification lists a very small value, though displayed in %FS.

In pressure measurement cells, the linearity is dependent on several factors:

  • the semiconductor resistors must be sufficiently small and diffused onto the exact right spot on the silicon diaphragm,
  • the silicon diaphragm has to be clean, sharp-edged and in exactly the right place,
  • linearity is varied, whether positive or negative pressure is measured, meaning whether the diaphragm bulges into a concave or a convex form (tensile or compression load),
  • the diameter to thickness ratio of the silicon diaphragm must be within a particular range. Very thin diaphragms will deform with superposed stretching: This balloon-effect, in transducers for lower pressure ranges, leads to a typically S-shaped course of the linearity curve (which cannot be rectified by analog compensation methods).
  • with very thick silicon diaphragms, the intended structure of the diaphragm, rigidly fixed at its edges, is no longer achievable, since, for example, with a 1,000 bar transducer, the diaphragm is half as thick as the chip itself.

The overload and burst pressure of piezoresistive pressure sensors

The typical course of a linearity curve is for the most part quite linear and then more heavily flattened. In the interest of as broad an output signal as possible, the longest possible extent of this curve is utilized. Until around two thirds mark, the course is so linear that error is less than 0.5 %FS. Beyond here, the linearity error becomes rapidly more dominant so that a limit from the accuracy is set. Aside from very low and very high pressure ranges, the nominal pressure range can be exceeded by typically around 50% before the measuring cell fails.

To increase overload protection, the idea of a broad effective signal has to be abandoned: A pressure sensor has to be employed, which would in itself be intended for a higher pressure range. Whilst, for example, a mechanical stop can be deployed in capacitive pressure sensors for its membrane deforming under pressure and a very high overload protection ensured, this is barely possible with the comparatively tiny silicon membranes of piezoresistive pressure cells with their most minimal of deflections.

At STS, the burst pressure is defined as the pressure at which a medium can enter the sensor and hence the metallic diaphragm is destroyed. The transducer, however, is already no longer functional at this point. Using Submersible Sensors the housings, cable connectors and cables are definitive. Burst pressure values of the transducer in the datasheet are thus negligible.

Contact

Subscribe To Our Newsletter

Join our mailing list to receive the latest news and updates from our team.

You have Successfully Subscribed!